Camera matching, or camera calibration, is the process of estimating camera parameters from certain features in an image. fSpy computes the approximate focal length, orientation and position of the camera in 3D space based on user defined control points in still images. The computed camera parameters can be used in other apps, for example 3D modeling tools.
A vanishing point is a point in a perspective image where all lines that are parallel in 3D space meet. For example, the tracks in the image below are parallel in the real world and meet in a single vanishing point.

The tracks meet at the vanishing point
fSpy uses the position of vanishing points to estimate camera parameters. A vanishing point is specified using two line segements aligned with features in the image that correspond to parallel lines in 3D space. The image below shows two such segements and the corresponding vanishing point, indicated as the intersection of the two thinner lines.

Specifying a vanishing point using two line segments
When the line segements are near-parallel, the vanishing point position cannot be computed accurately. The larger the angle between the line segments, the better.
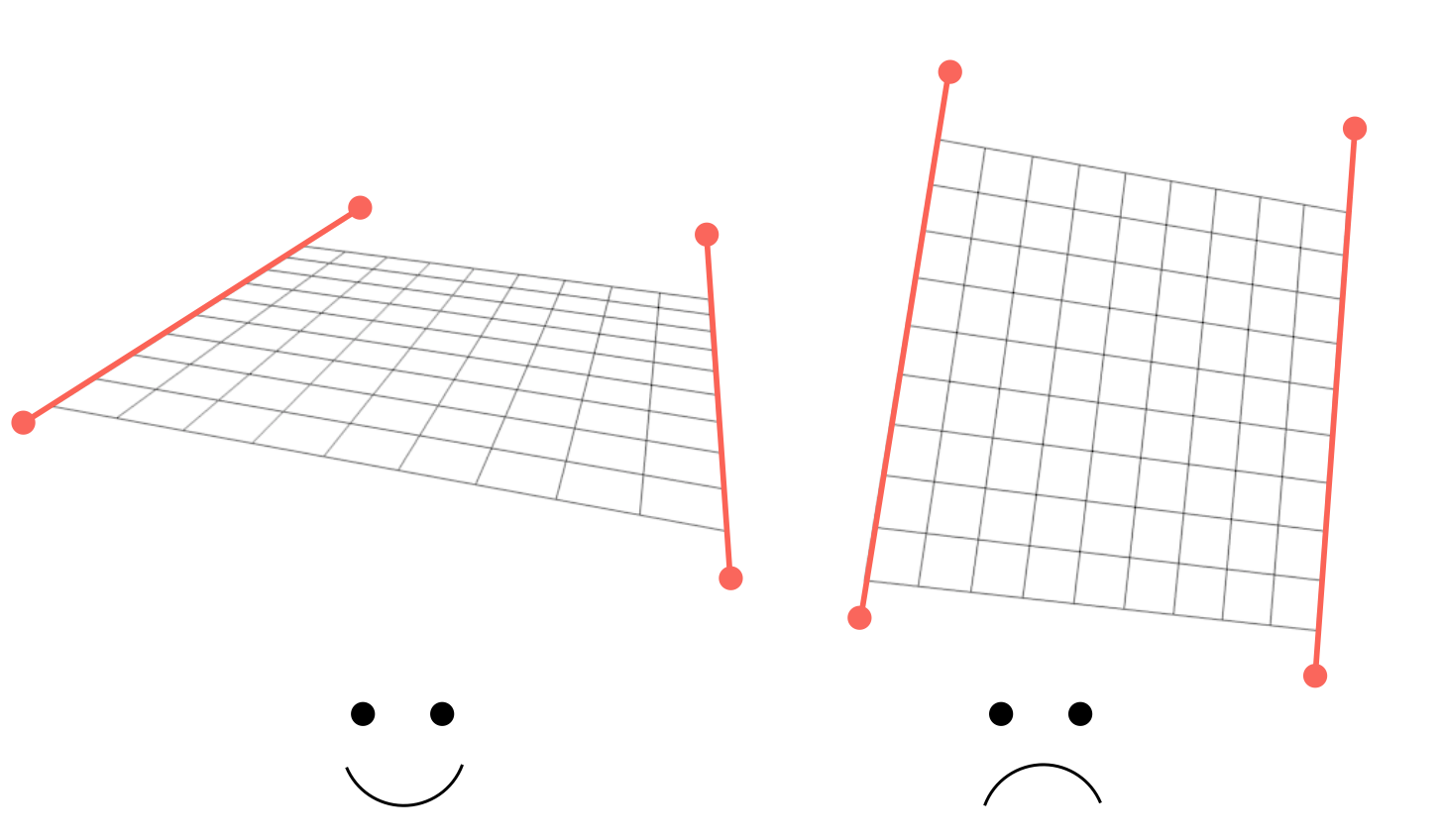
Larger angle between line segments means more accurate vanishing point calculation
Vanishing points in fSpy are assumed to correspond to perpendicular directions in 3D space, i.e directions at mutually right angles.
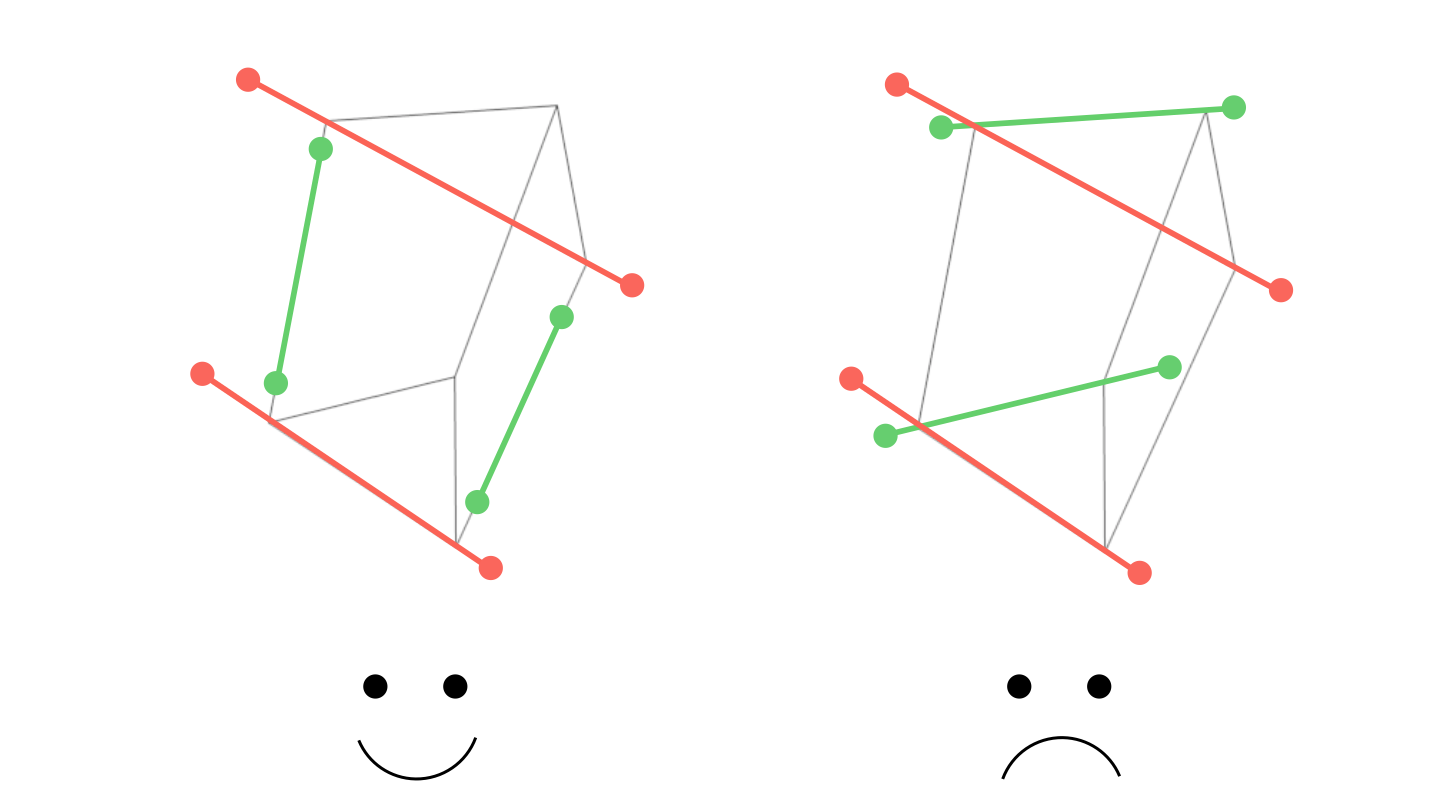
Vanishing points for perpendicular directions (left) and non-perpendicular directions (right)
fSpy only works with perspective images resulting from some pinhole camera like process. Suitable images include
The following types of images will not work well with fSpy